Wang, F., Xiang, X., Cheng, J., & Yuille, A. L. (2017, October). Normface: l 2 hypersphere embedding for face verification. In Proceedings of the 2017 ACM on Multimedia Conference (pp. 1041-1049). ACM.
NormFace 主要从理论分析层面理解人脸识别中归一化 (Normalization) 问题。文献提出了两种策略是:
- 修改 softmax loss, 使用 cosine 相似度替代内积
- 引入每一类的 agent vector 改写度量学习
Introduction
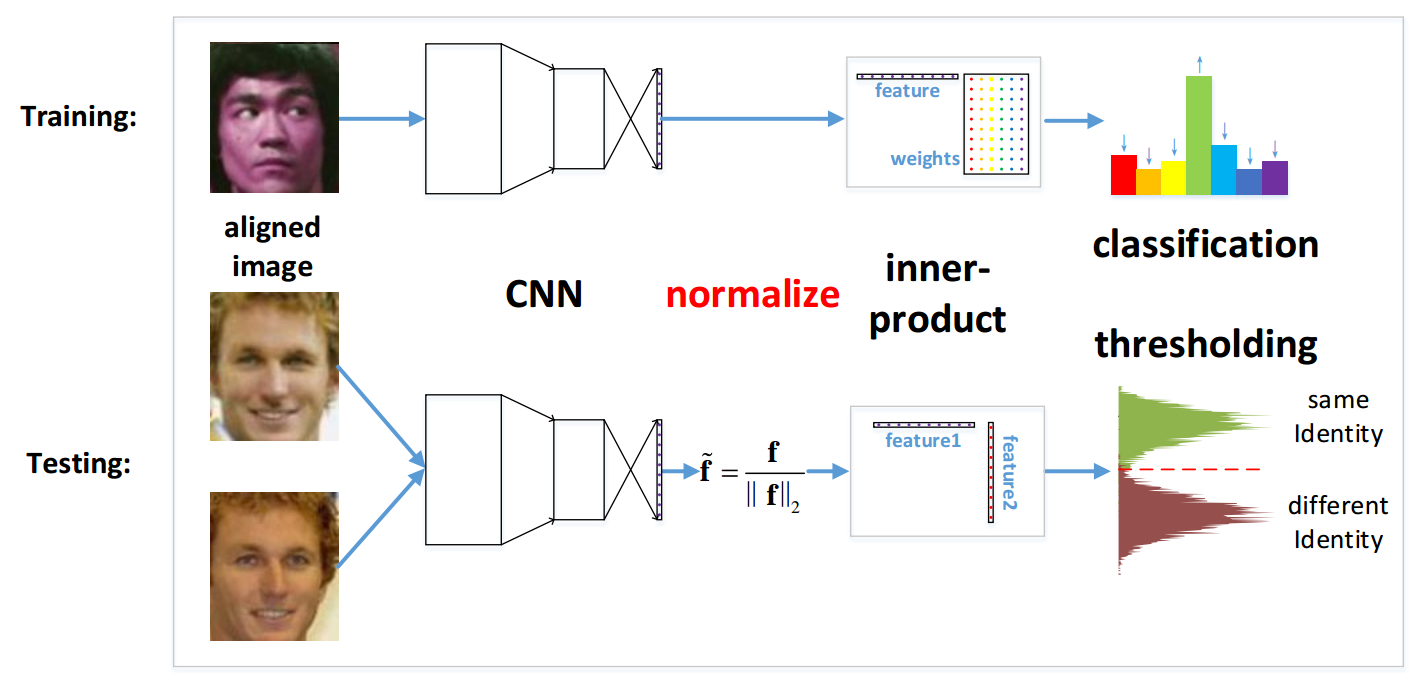
Face Varification 阶段的一般性做法: 使用 cosine 相似度或者等效的 L2 归一化欧氏距离。作者认为到目前为止,还没有研究人员明确解释为何在测试阶段需要对特征进行归一化。
作者实验发现,归一化 embedding 层和全连接层的权重,网络很难收敛。
文章解决了如下四个问题:
- 为何特征归一化有效?
- 为何使用 softmax loss 直接优化 cosine 相似度会失效?
- 怎样使用 softmax loss 优化 cosine 相似度?
- 是否有其他损失函数适合做 feature normalization?
Two tricks:
- 原始图像和镜像图像通过加的形式特征融合;
- 对于视频对,使用人脸相似性直方图
L2 Normalization Layer
- 为何需要特征归一化
- 直接对归一化特征使用softmax loss 为何难收敛
归一化必要性
Softmax-loss 定义:
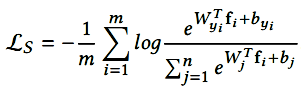
其中 $\mathbf{f}_i$ 是第 i 个样本的特征。
命题 1: 剔除偏置项 $b$, 有 $P_i(s\mathbf{f})\geq P_i(\mathbf{f})$. 即是说一般情况下,特征幅值越大,softmax loss 的分类性能就会越好。
在文章中因为通过了归一化, 并未使用到放大尺度特性。为了避免某些类的重叠,在分类层会去掉偏置项。
层定义
定义:
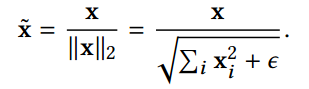
求导:
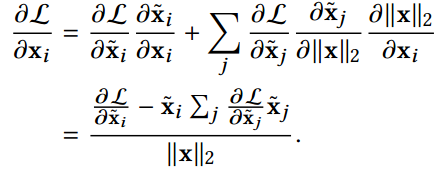
特性: $\mathbf{x}$ 与 $\partial L/\partial\mathbf{x}$ 正交。
改写 Softmax loss
L2 归一化之后, conine 距离 $d(\mathbf{f}, \mathbf{W}_i)$ 的阈值范围为 [-1, 1], 这样会导致即使在已经良好分类的情况下,概率 $P_{y_i}=e^{W^T_{y_i} f}/\sum{e^{W^T_j f}}$ 很难达到 1.
命题 2: 归一化后 Softmax Loss 下界问题 —— 特征和权重的每列归一化后,其范数为 $l$, 则 softmax loss 具有下界: $\log(1 + (n-1) e^{-\frac{n}{n-1}l^2})$.
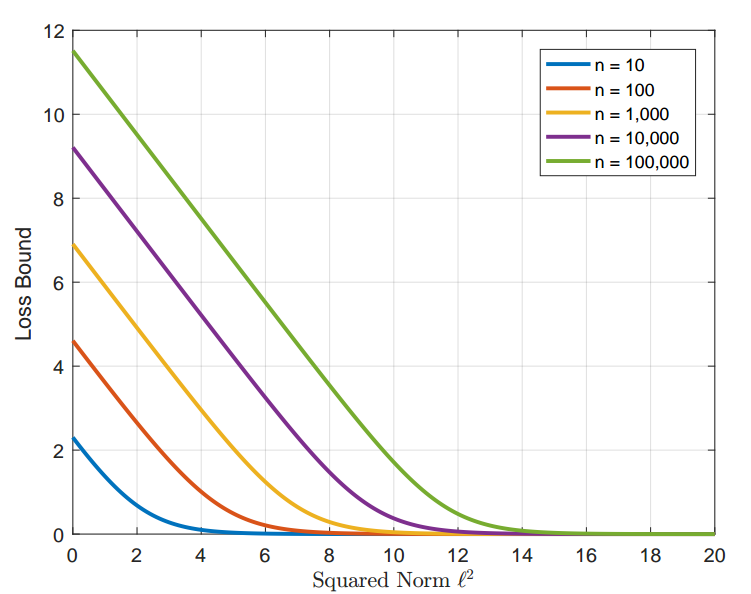
命题 2 即是说如果仅归一化 features 和 weights 为 1, 在训练集上 softmax loss 将会陷入非常高的值。若需要 loss 继续下降,则可以归一化特征和权重到一个更大的的值 $l$, 而不是 1.
实际操作中,可以令 $s = l^2$, $s$ 的值根据类别数的多少来确定。为了使参数也能自动学习,修改后的关于 cosine 距离的 softmax loss 定义为:
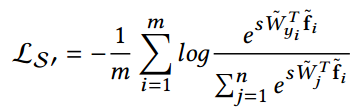
其中,$\mathbf{\tilde{f}}$ 是归一化特征。
重塑 Metric Learning
由 $|\mathbf{\tilde{f}}_i - \tilde{W}_i|_2^2=2 - 2\mathbf{\tilde{x}}^T\mathbf{\tilde{y}}$, 则有规范化的欧氏距离:
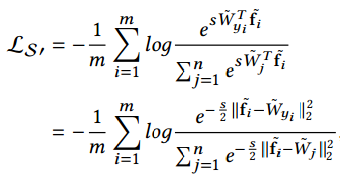
定义 $\tilde{W}_i$ 为第 i 类的代理 (agent), 修改后分类版的 contrastive loss:
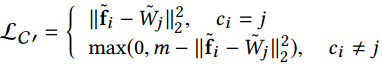
triplet loss:
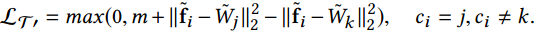
需要注意的是,如果使用原始版本一样的 margin, 那么有些临界特征不能被很好分类。所以需要设置更大的 margin.
Experiments
- features 和 weights 的列向量采用 L2-normalization.